TÍNH TOÁN LỢI TỨC ĐẦU TƯ – PHẦN 2

PHẦN 2 – TÌM HIỂU BA PHƯƠNG PHÁP
Để giúp bạn thấy các bước trên vận hành ra sao trong thực tế, chúng ta sẽ nghiên cứu một ví dụ đơn giản. Công ty của bạn đang cân nhắc mua một thiết bị có giá 3.000 $ – chẳng hạn như một chiếc máy tính chuyên dụng giúp giảm thời gian giao dịch giữa nhân viên và khách hàng. Công ty kỳ vọng có thể sử dụng chiếc máy tính này trong 3 năm. Ước tính, cuối mỗi năm, chiếc máy tính sẽ mang về cho công ty 1.300 $. Tỷ suất lợi tức yêu cầu – tức tỷ suất sinh lợi tối thiểu – mà công ty đặt ra là 8%.
Vậy, bạn có mua chiếc máy tính này không?
Phương pháp tính thời gian hoàn vốn
Phương pháp tính thời gian hoàn vốn có lẽ là cách thức đơn giản nhất để đánh giá dòng tiền tương lai mà một khoản đầu tư cơ bản mang lại. Nó đo lường thời gian cần thiết để dòng tiền mà dự án tạo ra có thể hoàn vốn cho khoản đầu tư ban đầu – hay nói cách khác, nó cho ta biết phải mất bao lâu mới có thể thu hồi vốn bỏ ra.
Thời gian hoàn vốn rõ ràng phải ngắn hơn tuổi đời của dự án; nếu không, chẳng có lý do gì để đầu tư cả. Trong ví dụ của chúng ta, bạn sẽ lấy khoản đầu tư ban đầu là 3.000 $ và chia cho dòng tiền thu được mỗi năm để tính thời gian hoàn vốn:
Chúng ta biết rằng thiết bị này sẽ được sử dụng trong 3 năm, nên thời gian hoàn vốn đã đáp ứng được bài kiểm tra đầu tiên: ngắn hơn tuổi đời của dự án. Điều mà chúng ta chưa tính đến là thiết bị sẽ mang lại bao nhiêu lợi nhuận trong suốt tuổi đời nó được sử dụng.
Ngay ở đây bạn có thể thấy ưu điểm cũng như nhược điểm của phương pháp tính thời gian hoàn vốn. Ưu điểm là việc tính toán và giải thích rất đơn giản. Nó là một cách đối chiếu thực tế nhanh chóng và dễ dàng. Nếu dự án bạn đang xem xét có thời gian hoàn vốn rõ ràng lâu hơn tuổi đời của dự án, có thể bạn chẳng cần phải xem xét gì thêm. Nếu nó có thời gian hoàn vốn nhanh hơn, bạn mới có lý do chính đáng để khảo sát sâu hơn. Đây là phương pháp thường được sử dụng trong các cuộc họp để xác định nhanh chóng liệu một dự án có đáng khai thác hay không.
Nhược điểm của phương pháp này là cung cấp rất ít thông tin. Nói cho cùng, một doanh nghiệp khi đầu tư không đơn thuần muốn chỉ dừng lại ở mức hòa vốn; doanh nghiệp luôn muốn có lợi nhuận. Phương pháp này không đánh giá được liệu dòng tiền có vượt qua được điểm hòa vốn không, cũng không cho bạn biết tổng lợi nhuận có thể là bao nhiêu. Nó cũng không tính đến giá trị thời gian của tiền. Nó có so sánh ngân sách phân bổ tiền mặt ngày hôm nay với dòng tiền dự kiến của ngày mai, nhưng quả thật đó chỉ là so sánh táo với cam, bởi một đồng của hôm nay có giá trị khác hẳn với một đồng của ngày mai.
Vì những lý do này, phương pháp tình thời gian hoàn vốn chỉ nên được sử dụng để so sánh các dự án (để bạn biết dự án nào sẽ hoàn vốn đầu tư sớm hơn) hoặc để loại dự án (những dự án không bao giờ hoàn được vốn đầu tư). Nhưng hãy nhớ, cả hai con số được dùng trong phép tính này đều được ước tính. Nghệ thuật tính toán ở đây là nhóm các con số lại với nhau – bạn có thể tiến đến gần việc định lượng một số không biết như thế nào? Vì vậy phương pháp tính thời gian hoàn vốn là quy tắc mang tính kinh nghiệm dạng thô sơ, chứ không phải một phân tích tài chính hùng hồn. Nếu thời gian hoàn vốn trông đầy hứa hẹn, hãy chuyển sang phương pháp tiếp theo để xem dự án đó có thật sự đáng đầu tư không.
Phương pháp giá trị hiện tại ròng
Phương pháp giá trị hiện tại ròng phức tạp hơn phương pháp tính thời gian hoàn vốn, nhưng nó cũng mạnh hơn; trên thực tế nó là lựa chọn đầu tiên của các chuyên gia tài chính khi phân tích các khoản mục đầu tư cơ bản. Lý do là gì?
- Thứ nhất, nó có tính đến giá trị thời gian của tiền, khấu trừ đi dòng tiền tương lai để thu về giá trị hiện tại.
- Thứ hai, nó xem xét chi phí vốn hoặc tỷ lệ lợi tức tối thiểu khác của doanh nghiệp.
- Thứ ba, nó cung cấp câu trả lời về giá trị của tiền ngày hôm nay, do đó cho phép bạn so sánh kế hoạch phân bổ ngân sách với giá trị hiện tại của khoản lợi nhuận có khả năng thu về.
Phương trình khấu trừ có dạng như sau:
Trong đó:
PV = giá trị hiện tại
FV = dòng tiền dự kiến trong mỗi giai đoạn thời gian
i: mức khấu trừ hoặc tỷ lệ lợi tức tối thiểu
n: số giai đoạn đang xem xét
Giá trị hiện tại ròng đơn giản bằng với giá trị hiện tại trừ đi ngân sách tiền mặt ban đầu. Đối với ví dụ mà chúng ta đang xem xét đến, các phép tính sẽ có dạng như sau:
Và:
NPV = 3.350 $ – 3.000 $ = 350 $
Diễn giải bằng câu chữ thì tổng dòng tiền kỳ vọng 3.900 $ trong tương lai sẽ chỉ có giá trị bằng 3.350 $ của ngày hôm nay với tỷ lệ khấu trừ là 8%. Sau khi trừ đi ngân sách tiền mặt ban đầu 3.000 $, ta sẽ có giá trị hiện tại tròng là 350 $.
Ta nên hiểu điều này như thế nào? Nếu giá trị hiện tại ròng của một dự án lớn hơn 0, dự án đó nên được thông qua, bởi thu nhập thu về đã lớn hơn ngưỡng hòa vốn. Ở đây, con số lợi nhuận 350 $ cho thấy dự án có lợi tức cao hơn 8%.
Một doanh nghiệp có thể thực hiện phép tính NPV với nhiều tỷ lệ khấu trừ. Nếu rơi vào trường hợp này bạn sẽ thấy mối quan hệ sau:
- Khi lãi suất tăng, NPV giảm
- Khi lãi suất giảm, NPV tăng
Mối quan hệ này kéo dài vì lãi suất càng cao nghĩa là chi phí cơ hội đối với ngân sách cũng cao hơn. Nếu thủ quỹ doanh nghiệp đặt ngưỡng thu hồi vốn là 20%, điều này có nghĩa là người thủ quỹ đó khá tự tin với việc thu được con số tương tự ở bất kỳ đâu với mức độ rủi ro tương tự. Vụ đầu tư mới thật sự tốt mới có thể hoàn được vốn. Ngược lại, nếu người thủ quỹ chỉ có thể thu được 4% ở những nơi khác, thì những vụ đầu tư mới trông khả quan sẽ nhiều hơn. Cũng tương tự như Quỹ Dự trữ Liên bang kích thích nền kinh tế Mỹ bằng cách giảm lãi suất, doanh nghiệp cũng có thể kích thích đầu tư nội bộ bằng cách hạ ngưỡng thu hồi vốn (hiển nhiên, làm việc này không phải là một chính sách khôn ngoan).
Một nhược điểm của phương pháp tính giá trị hiện tại ròng là rất khó giải thích và trình bày với người khác. Thời gian hoàn vốn thì dễ hiểu, nhưng giá trị hiện tại ròng lại là con số dựa trên giá trị đã khấu trừ của dòng tiền tương lai – đây rõ ràng không phải là cụm từ mà những người làm ngoài lĩnh vực tài chính có thể dễ dàng thốt ra. Tuy nhiên, một nhà quản lý muốn trình bày về NPV phải kiên quyết đến cùng.
Giả sử ngưỡng thu hồi vốn bằng hoặc lớn hơn chi phí đầu tư cơ bản của doanh nghiệp, bất kỳ vụ đầu tư nào vượt qua được bài kiểm tra giá trị hiện tại ròng sẽ gia tăng được giá trị cổ đông, và bất kỳ vụ đầu tư nào thất bại, nếu vẫn cứ được tiến hành, sẽ gây tổn thất cho doanh nghiệp và cổ đông.
Một nhược điểm tiềm ẩn khác – đây cũng là nghệ thuật tài chính – đơn giản là các phép tính NPV dựa trên quá nhiều ước tính và giả định. Ta chỉ có thể ước tính các phỏng đoán về dòng tiền. Chi phí ban đầu của một dự án có thể khó xác định. Và tất nhiên, những mức khấu trừ khác nhau sẽ cho ra những NPV hoàn toàn khác nhau. Tuy vậy, càng hiểu rõ phương pháp này, bạn sẽ càng có khả năng đặt câu hỏi về giả định của những người khác – và sẽ dễ dàng cho bạn khi chuẩn bị các đề án, đưa ra những giả định mà bạn có thể bảo vệ. Người khác – cấp trên, giám đốc điều hành, bất cứ ai khác – cũng sẽ thấy ẽo trí tuệ tài chính của bạn khi trình bày và giải thích NPV trong cuộc họp thảo luận về một khoản mục đầu tư vốn cơ bản. Hiểu biết của bạn về phân tích này sẽ cho phép bạn tự tin giải thích tại sao nên tiến hành đầu tư, hay tại sao không.
Phương pháp tính tỷ suất sinh lời nội bộ
Việc tính toán tỷ suất sinh lời nội bộ cũng tương tự như tính giá trị hiện tại ròng, chỉ có biến số được sử dụng là khác. Thay vì giả định một tỷ lệ khấu trừ cụ thể, rồi kiểm tra giá trị hiện tại của khoản đầu tư, IRR tính toán tỷ suất sinh lời thực tế từ dòng tiền dự kiến. Người ta có thể so sánh tỷ suất sinh lời này với ngưỡng thu hồi vốn của doanh nghiệp để xem dự án đầu tư có vượt qua được bài kiểm tra hay không.
Trong ví dụ của chúng ta, công ty đang đưa ra đề xuất đầu tư 3.000 $, và trong ba năm tiếp theo, mỗi năm công ty sẽ nhận được 1.300 $ tiền mặt. Bạn không thể chỉ đơn thuần sử dụng tổng dòng tiền 3.900 $ đó để tính toán TSSL, bởi lợi nhuận đó được trải ra cả 3 năm. Vì vậy, chúng ta cần thực hiện một số phép tính.
Trước hết, đây là một cách để tìm hiểu IRR: đó là ngưỡng thu hồi vốn làm cho giá trị hiện tại ròng bằng 0. Bạn nhớ chúng tôi đã nói rằng khi tỷ lệ khấu trừ tăng, thì NPV giảm? Nếu bạn thực hiện các phép tính NPV với lãi suất mỗi lúc một cao hơn, bạn sẽ thấy NPV mỗi lúc một nhỏ hơn, cho đến khi âm, có nghĩa là dự án không vượt qua được ngưỡng thu hồi vốn. Trong ví dụ, nếu bạn có đặt ngưỡng thu hồi vốn là 10%, bạn sẽ thu được giá trị hiện tại ròng vào khoảng 212 $. Nếu bạn thử 20%, giá trị hiện tại ròng của bạn sẽ âm, ở mức -218 $. Vì vậy, điểm tới hạn mà tại đó NPV bằng 0 sẽ nằm đâu đó trong khoảng từ 10% – 20%. Theo lý thuyết, bạn có thể tiếp tục thu hẹp khoảng cách này cho đến khi tìm ra con số cụ thể. Trên thực tế, bạn có thể sử dụng một bộ tính tài chính hoặc một công cụ web, và bạn sẽ thấy điểm mà tại đó NPV bằng 0 là 14,36%. Đây chính là TSSL nội bộ của dự án đầu tư.
IRR là phương pháp dễ trình bày và giải thích, bởi nó cho phép so sánh nhanh lợi tức từ dự án với ngưỡng thu hồi vốn. Nhược điểm của nó là nó không định lượng đóng góp của dự án vào tổng thể của doanh nghiệp như phương pháp NPV. Nó cũng không định lượng có tác động của một biến quan trọng, cụ thể là thời gian mà doanh nghiệp có thể hưởng TSSL đó. Khi các dự án cạnh tranh có thời gian thực hiện khác nhau, việc sử dụng IRR có thể dẫn bạn tới chỗ thiên vị những dự án có thời gian hoàn vốn nhanh, TSSL cao, trong khi lẽ ra bạn nên đầu tư vào những dự án có thời gian hoàn vốn dài hơn và TSSL thấp hơn. IRR cũng không giải quyết được vấn đề quy mô. Ví dụ, TSSL 20% không cho bạn biết bất kỳ điều gì về quy mô dòng tiền thu về. Nó có thể là 20% của một đồng, nhưng cũng có thể là 20% của một triệu đồng. Trong khi đó, NPV có thể cho bạn biết con số thu hồi có thể là bao nhiêu. Nói tóm lại, khi khoản đặt cược cao, sử dụng cả IRR à NPV sẽ hợp lý hơn.
Trích từ sách Financial Intelligence, tác giả Karen Berman, Joe Knight, John Case
Mời bạn xem tiếp >>> TÍNH TOÁN LỢI TỨC ĐẦU TƯ – PHẦN 3
|
MỜI MUA ĐẤT NỀN TÂY NINH
|
 |


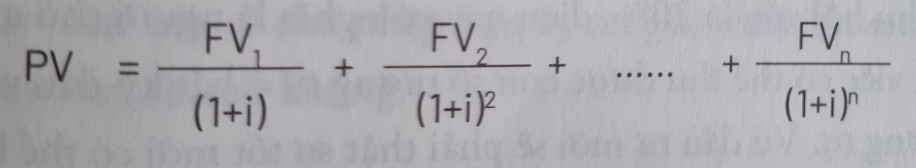
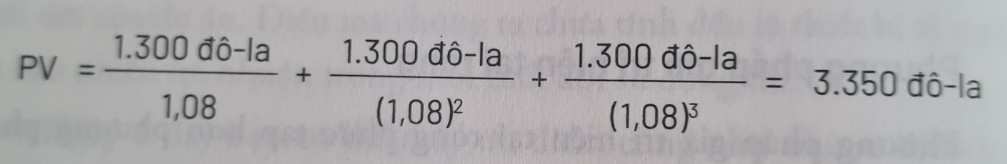



Tham gia thảo luận